
Sommario
Tecniche di clustering
In questo articolo parleremo del significato del termine Cluster, e cosa si intende per cluster analysis.
Il clustering consiste in un insieme di metodi per raggruppare oggetti in classi omogenee. Un cluster è un insieme di oggetti che presentano tra loro delle similarità, ma che, per contro, presentano dissimilarità con oggetti in altri cluster. L’input di un algoritmo di clustering è costituito da un campione di elementi, mentre l’output è dato da un certo numero di cluster in cui gli elementi del campione sono suddivisi in base a una misura di similarità. Gli algoritmi di clustering forniscono come output anche la descrizione delle caratteristiche di ciascun cluster, il che è fondamentale per poi prendere decisioni strategiche sulle azioni da compiere verso tali gruppi (marketing mirato, promozioni ad-hoc, creazione di nuovi prodotti/servizi).
Utilizzo della clustering analysis
La cluster analysis è utilizzata per numerose applicazioni:
- Ricerche di mercato.
- Riconoscimento di pattern.
- Raggruppamento di clienti in base ai comportamenti d’acquisto (segmentazione del mercato).
- Posizionamento dei prodotti.
- Analisi dei social network, per il riconoscimento di community di utenti.
- Identificazione degli outliers. Gli outliers sono valori anomali che presentano grandi differenze con tutti gli altri elementi di un data set. La loro identificazione può essere interessante per due scopi: l’eliminazione di questi valori anomali, che potrebbero essere causati da errori, oppure l’isolamento di questi casi particolari che magari rivestono una certa importanza per il business.
Algoritmi di clustering
Gli algoritmi di clustering si dividono in due categorie principali:
- Algoritmi di clustering gerarchico
- Algoritmi di clustering partizionale
I primi organizzano i dati in sequenze nidificate di gruppi che potremmo rappresentare in una struttura ad albero. Gli algoritmi di clustering partizionale, invece, determinano il partizionamento dei dati in cluster in modo da ridurre il più possibile la dispersione all’interno del singolo cluster e, viceversa, di aumentare la dispersione tra un cluster e un altro. Non si tratta in questo caso di algoritmi gerarchici, poiché i cluster sono tutti allo stesso livello di partizionamento.
Gli algoritmi di clustering partizionali sono più adatti a data set molto grandi, per i quali la costruzione di una struttura gerarchica dei cluster porterebbe a uno sforzo computazionale molto elevato. Per questo, nel prosieguo del post ci occuperemo in modo più approfondito di questa tecnica.
Misure di similarità per la clustering analysis
La misura di similarità tra un elemento e un altro può essere calcolata con metodi diversi.
Esistono numerose misure di similarità, tra le quali ricordiamo la distanza di Minkowski, il Simple Matching Coefficient, il coefficiente di Jaccard, la Pearson’s correlation.
Una delle misure più semplici è la distanza euclidea tra due punti in uno spazio n-dimensionale. La sua formula è:
dove:
xi e xj sono due elementi del data set rappresentati da vettori. Per es.: xi = {xi1, xi2, …, xin} n è il numero di dimensioni
La formula è valida per le variabili continue, mentre per i valori booleani (vero/falso) o per le variabili categoriche (per es. il colore che potrebbe essere verde, bianco, rosso, ecc..) si utilizza un’altra formula:
p è il numero di attributi booleani o categorici
m è il numero di attributi con lo stesso valore tra xi e xj
Clustering gerarchico di tipo agglomerativo
Il clustering gerarchico di tipo agglomerativo utilizza l’algoritmo seguente per l’identificazione dei cluster:
- Inizialmente ciascun elemento del data set forma un cluster separato
- Ad ogni iterazione sono accorpati i cluster più simili, via via ampliando la soglia di similarità
- L’iterazione termina quando tutti gli oggetti sono accorpati in un unico cluster, dove tutti gli elementi sono considerati simili.
La formazione dei cluster è rappresentata attraverso un dendogramma, o grafico a albero, come mostra la figura seguente:
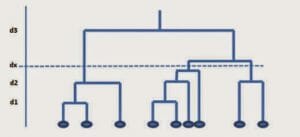
Il punto di taglio dell’albero, definito dall’utente e rappresentato in figura con il valore di distanza dx, determina il numero di cluster. L’algoritmo è accurato ma è poco efficiente dal punto di vista del calcolo. Inoltre non prevede una riassegnazione degli elementi ai cluster durante l’iterazione.
Clustering partizionale
Vediamo ora come funziona il clustering partizionale. Innanzitutto occorre stabilire quanti cluster si vogliono avere e indichiamo tale numero con K. Il procedimento è il seguente:
1) Partizioniamo l’insieme in K cluster, assegnando a ciascuno di essi degli elementi scelti a caso.
2) Calcoliamo i centroidi di ciascun cluster k con al formula seguente:
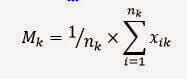
Mk è il vettore delle medie, o centroide per il cluster k
nk è il numero di elementi del cluster k
xik è l’i-esimo elemento del cluster3) Calcoliamo la distanza degli elementi del cluster dal centroide, ottenendo un errore quadratico, attraverso la formula
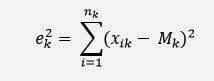
ek2 è l’errore quadratico per il cluster k
xik è l’i-esimo elemento del cluster
nk è il numero di elementi del cluster k
Mk è il vettore delle medie, o centroide per il cluster k.
K-means vs. K-medoids
A. Rezzani, Business Intelligence. Processi, metodi, utilizzo in azienda, APOGEO, 2012Mehmed Kantardzic Data Mining: Concepts, Models, Methods, and Algorithms, John Wiley & Sons, 2003
Jiawei Han, Micheline Kamber, Data Mining:Concepts and Techniques Second Edition, Morgan Kaufmann Publishers, 2006

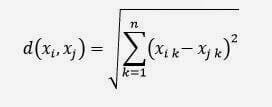
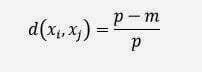





Leave A Comment